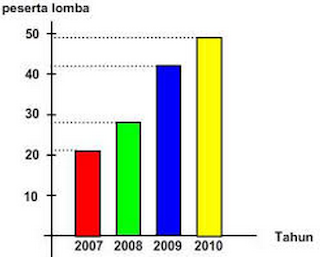
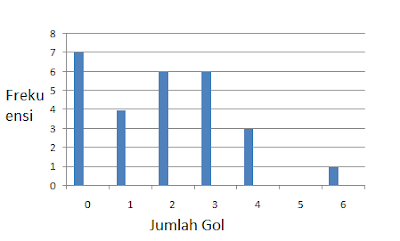
Penyajian Data Menggunakan Diagram Garis

Penyajian Data Menggunakan Diagram Garis – Bila dalam artikel Rumus Matematika Dasar sebelumnya telah dibahas mengenai Diagram Batang, kali ini kita akan mempelajari cara penyajian data yang cukup mirip dengan diagram batang yakni dengan menggunakan diagram garis. Diagram garis biasanya digunakan untuk menyajikan data yang diperoleh dari waktu-ke waktu secara teratur dengan interval waktu tertentu. Biasanya diagram garis dipergunakan untuk mengetahui perkembangan atau pertumbuhan dari suatu hal secara kontinu (berkelanjutan). Misalnya, pertumbuhan tinggi pohon mangga setiap bulan, perkembangan berat badan bayi setiap bulan, dan banyaknya curah hujan di suatu daerah dalam kurun waktu setahun. Berikut adalah contoh diagram garis.

Mirip dengan diagram batang, di dalam diagram garis juga dipergunakan sumbu mendatar dan juga sumbu tegak dimana keduanya saling berpotongan secara tegak lurus. Pada umumnya, sumbu mendatar menunjukkan lama waktu pengamatan sedangkan sumbu tegak menunjukkan hasil dari pengamatan yang dilakukan. Pasangan nilai pada sumbu mendatar dan sumbu tegak digambarkan dengan sebuah titik layaknya titik yang digunakan pada diagram cartesius. Kemudian titik-titik itu dihubungkan satu-persatu sehingga membentuk sebuah garis/kurva.

Penyajian Data Menggunakan Diagram Garis

Mari kita pelajari bersama ara menggambar diagram garis dengan mengamati contoh soal yang ada di bawah ini:

Contoh Soal:

Berikut ini adalah tabel nilai rata-rata Ujian Nasional SMP Harapan Bangsa dalam kurun waktu 6 tahun terakhir:

Coba sajikan data tersebut dengan menggunakan diagram garis!

Penyelesaian:

Itulah kiranya tata cara Penyajian data dengan menggunakan diagram garis. Penyajian data dengan metode ini cenderung lebih mudah dibandingkan dengan jenis diagram yang lain karena kita hanya tinggal menentukan titik-titik sesuai dengan data yang diperoleh kemudian titik-titik tersebut kita hubungkan sehingga membentuk garis yang berbentuk kurva.

Penyajian Data Menggunakan Diagram Lingkaran

Penyajian Data Dengan Diagram Lingkaran – Penyajian data bisa dilakukan dengan banyak cara. Selain dengan menggunakan tabel, piktogram, ataupun diagram batang penyajian data juga bisa dilakukan dengan menggunakan diagram lingkaran. Pada kesempatan kali ini Rumus Matematika Dasar akan melanjutkan materi mengenai penyajian data dengan membahas lebih jauh tentang diagram lingkaran dan langkah-langkah pembuatannya. Diagram lingkaran biasanya digunakan untuk menyajikan data dalam bentuk persentase. Daerah lingkaran menggambarkan keseluruhan data. Data disajikan dengan menggunakan juring atau sektor dimana besar sudut pusat juring sesuai dengan perbandingan tiap-tiap data terhadap keseluruhan data yang ada. Berikut adalah contoh diagram lingkaran:

Penyajian Data Menggunakan Diagram Lingkaran

Untuk mempelajari langkah-langkah penyajian data dengan menggunakan diagram lingkaran kalian bisa langsung mengamati contoh soal yang ada di bawah ini:

Contoh Soal:

Di dalam sebuah kelas terdapat siswa sebanyak 60 orang. Masing-masing siswa diwajibkan untuk memiliki setidaknya satu jenis kegiatan ekstrakulikuler. Setelah dikumpulkan, diperoleh data yaitu 15 orang siswa memilih basket, 17 siswa memilih bola voli, 24 siswa memilih futsal, dan 4 orang memilih Pramuka. Buatlah diagram ,ingkaran dari data tersebut!

Penyelesaian:

Sebelum membat diagram lingkaran dari data tersebut, kita harus mencari persentasenya terlebih dahulu sehingga nantinya kita bisa menentukan besarnya sudut dari masing-masing data yang diperoleh.

Setelah kita peroleh persentase dan besar sudutnya, kita bisa menyajikan data tersebut ke dalam diagram lingkaran seperti di bawah ini:

Demikianlah ulasan dan rangkuman materi tentang cara Penyajian Data Menggunakan Diagram Lingkaran semoga pembahasan contoh soal di atas bisa membuat kalan paham tentang langkah-langkah yang harus dilakukan ketika ingin menyajikan data dalam bentuk diagram lingkaran dimana data-data yang diperoleh digambarkan dalam bentuk persentase dan besar sudut di salam sebuah lingkaran.

Lingkaran dan Unsur-Unsur Lingkaran

Lingkaran
Lingkaran adalah kumpulan titik yang mempunyai jarak sama terhadap suatu titik tertentu (disebut titik pusat). Jarak tertentu tersebut dinamakan jari-jari.

Roda atau ban sepeda merupakan salah satu contoh bentuk lingkaran









  Secara Matematika (geometri) Gambar lingkaran seperti berikut.

Lingkaran sebagai kumpulan titik-titik yang banyak.

Titik-titik yang sangat banyak sehingga tampak seperti garis. Sehingga lingkaran disajikan seperti gambar di samping.






Unsur-Unsur Lingkaran

1. Jari-jari: jarak dari pusat lingkaran ke titik pada lingkaran. PA, PB, PC, dan PD merupakan jari-jari lingkaran P.

2. Tali busur: ruas garis yang menghubungkan dua titik pada lingkaran. AB merupakan tali busur lingkaran P.

3. Diameter: tali busur yang melalui pusat lingkaran. AC merupakan diameter dan tali busur terpanjang pada lingkaran P.

4. Apotema: jarak tali busur ke pusat lingkaran. EP merupakan apotema lingkaran P.

5. Busur: garis lengkung yang menghubungkan dua titik pada lingkaran. Busur merupakan bagian dari keliling lingkaran. Garis lengkung AB merupakan busur lingkaran P.

6. Juring: daerah yang dibatasi oleh dua jari-jari dan sebuah busur. Juring merupakan bagian dari luas lingkaran. Daerah PCD merupakan juring lingkaran P.

7. Tembereng: daerah yang dibatasi oleh sebuah tali busur dan busurnya. Daerah AFB merupakan sebuah tembereng.

Keliling dan Luas Lingkaran

 

Keliling = 2 x Phi x r

Luas = Phi x r x r 

        = Phi x r²

Dengan nilai Phi = 22/7 atau 3,14

 Sudut Pusat dan Sudut Keliling

∠APB merupakan sudut pusat.

∠ADB dan ∠ACB merupakan sudut keliling.

1. Jika menghadap busur yang sama, besar sudut pusat sama dengan dua kali besar sudut keliling. ∠APB = 2 × ∠ACB.

 2. Sudut keliling yang menghadap busur yang sama besarnya sama.

∠ADB = ∠ACB.

3. Sudut keliling yang menghadap diameter besarnya 90°.



Panjang Busur, Luas Juring, dan Luas Tembereng

Panjang busur, luas juring dan luas tembereng yang dibentuk oleh dua jari-jari dan sudut pusat tertentu dapat dihitung dengan rumus berikut. Misalkan jari-jari lingkaran dinyatakan dengan r.

Contoh 1

Diketahui lingkaran O dengan jari-jari 70 cm dan sudut pusat AOB = 72^o. Tentukan:

a. Panjang busur AB

b. Luas Juring AOB.

Jawaban :

Jadi,panjang busur AB = 88 cm.

Jadi, Luas Juring AOB =3.080 cm².

Penyajian Data Menggunakan Diagram Batang

Penyajian Data Menggunakan Diagram Batang – Sebelumnya Rumus Matematika Dasar telah memaparkan materi mengenai bagaimana cara menyajikan data menggunakan piktogram. Sekarang kita lanjutkan materi tersebut dengan cara penyajian data yang lain yaitu dengan menggunakan diagram batang. Tentunya kalian sudah tidak asing lagi dengan diagram batang seperti yang bisa dilihat pada contoh gambar berikut ini:

Mengapa disebut diagram batang? Tentu saja karena data-data yang telah dikumpulkan digambarkan dalam bentuk batang-batang. Tiap-tiap batang memiliki lebar yang sama namun tingginya bisa berbeda-beda bergantung kepada frekuensi dari data yang bersangkutan.

Penyajian Data Menggunakan Diagram Batang

Untuk membuat diagram batang kita akan memerlukan sumbu mendatar dan juga sumbu tegak yang keduanya saling berpotongan tegak lurus. Sumbu mendatar biasanya menyatakan jenis kategori yang digunakan untuk memisahkan data-data yang ada. Sedangkan sumbu yang tegak menunjukkan frekuensi dari data tersebut. Skala yang digunakan pada sumbu mendatar dan sumbu tegak tidaklah harus sama. Letak masing-masing batang harus dibuat terpisah dengan jarak yang sama. Coba kalian simak contoh soal dan pembahasan diagram batang di bawah ini:

Contoh Soal:

Selama satu tahun tim sepak bola Harapan Jaya bermain sebanyak 27 kali sementara jumlah gol yang mampu dicetak oleh kesebelasan tersebut di dalam setiap pertandingannya dapat dilihat pada tabel berikut. Buatlah diagram batangnya!

Penyelesaian:

Bila data tersebut diubah ke dalam diagram batang maka akan terlihat seperti ini:

Itulah penjelasan sederhana tentang Penyajian Data Menggunakan Diagram Batang. Untuk materi selanjutnya akan dibahas lebih jauh mengenai cara penyajian data yang lain yaitu mengenai diagram lingkaran. Oleh karena itu, ikuti terus pembahasan materi yang diberikan blog ini agar kalian dapat terus menambah pengetahuan mengenai beragam materi pelajaran matematika.