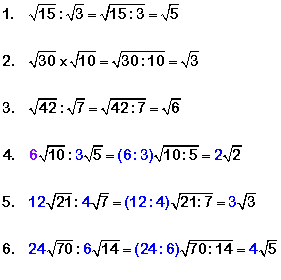Merasionalkan Penyebut pada Pecahan Bentuk Akar

Dalam kesempatan ini kita akan membahas tentang cara merasionalkan penyebut pecahan bentuk Akar. Bentuk pecahan berpenyebut bentuk akar seperti di bawah ini.

Bentuk bentuk pecahan di atas memiliki penyebut bentuk akar. Sehingga bentuk tersebut belum sederhana (lazim). Oleh karena itu, bentuk pecahan di atas harus disederhanakan. Pecahan bentuk akar sudah dikatakan sederhana (lazim) apabila memenuhi syarat berikut.
1. Setiap bilangan bentuk akar sudah ditulis paling sederhana
2. Penyebut pada pecahan berupa bilangan rasional atau bilangan bulat.
Nah, untuk itu kita akan membahas cara menyederhanakan berbagai bentuk pecahan di atas.

Sebelum merasionalkan penyebut pecahan bentuk akar, perlu diketahui bahwa akar sekawan bentuk akar mempunyai peran di sini. Akar sekawan tersebut berperan dalam merasionalkan bentuk-bentuk akar.
Ingat pola berikut.

Coba dicermati lagi, ternyata perkalian bentuk akar dengan sekawannya menghasilkan bilangan bulat. Nah, makanya perkalian di atas sangat berperan dalam merasionalkan penyebut pecahan bentuk akar.

Mari kita merasionalkan pecahan bentuk akar di atas.

1. Merasionalkan penyebut bentuk akar tunggal

2. Merasionalkan pecahan berpenyebut  operasi bilangan bulat dan bentuk akar

3. Merasionalkan pecahan berpenyebut bentuk operasi dua bilangan bentuk akar

Demikian sedikit penjelasan tentang merasionalkan penyebut dari pecahan berbentuk akar.

Semoga bermanfaat

Operasi Hitung Bentuk Akar

Operasi hitung bentuk akar merupakan materi kelas 3 SMP. Operasi hitung bentuk akar yang akan dipelajari kali  ini adalah menyederhanakan bentuk akar, operasi hitung (penjumlahan, pengurangan, perkalian, dan pembagian) bentuk akar.

Bilangan bentuk akar adalah bilangan yang memuat tanda akar  dan tidak bisa disederhanakan dalam bentuk bilangan cacah/bilangan asli. 
Contoh : perhatikan dan bedakan bentuk akar dan bilangan bukan bentuk akar.

Deretan bentuk akar bagian bawah bukan bentuk akar sejati karena akar-akar bilangan tersebut dapat disederhanakan menjadi bilangan cacah/asli, yaitu 1, 2, 3, 4, 5, dan 9.

 Menyederhanakan bilangan bentuk akar.
Kadang kala bentuk akar memuat bilangan yang besar dan dapat difaktorkan menjadi perkalian bilangan-bilangan tertentu. Jika terdapat bentuk akar yang demikian, maka bilangan-bilangan itu dapat disederhanakan.
Perhatikan contoh-contoh bentuk akar dan cara menyederhanakannya berikut.

Menjumlah dan Mengurangkan Bentuk Akar
Dalam menjumlah dan mengurangkan bentuk akar sangat mudah seperti pada bilangan bulat. Perlu diperhatikan bahwa operasi penjumlahan/pengurangan pada bentuk akar yang sejenis (Bilangan akarnya sama), maka hasilnya dapat diserhanakan. Sedangkan untuk bentuk akar yang sejenis tidak dapat disederhanakan. 
Lebih jelasnya perhatikan contoh-contoh berikut.

Jadi, secara umum dirumuskan sebagai berikut.

Mengalikan Bentuk Akar
Dalam mengalikan bentuk akar perlu diperhatikan pada bentuk bulat dan bentuk akarnya. Jika terdapat perkalian du bentuk akar, maka hasilnya bentuk akar dari perkalian kedua bilangan itu. Jika terdapat dua bilangan yang memuat bilangan bulatnya,kalikan bilangan bulat dengan bulat dan bentuk akar dengan bentuk akar. Begitu juga pada pembagiannya.
Lebih jelasnya perhatikan contoh-contoh berikut.

Jadi, secara umum dapat dirumuskan seperti berikut.

Membagi Bentuk Akar
Membagi bentuk akar sama mudahnya dengan mengalikan bentuk akar. Lebih jelasnya perhatikan beberapa contoh pembagian bentuk akar berikut.

Secara umum dapat dituliskan seperti berikut.

Merasionalkan Bentuk Akar
Pada dasarnya bentuk pecahan yang sering kita jumpai adalah pembilang dan penyebutnya berupa bilangan bulat. Walaupun demikian dalam bentuk akar juga terdapat pecahan bentuk akar. Namun, pada pecahan bentuk akar ada syarat-syarat yang menjadikan bentuk pecahan bentuk akar tersebut lazim untuk dituliskan. Pada pecahan bentuk akar, penyebutnya diussahakan berbentuk bilangan bulat. Jadi, apabila terdapat pecahan yang penyebutnya masih berbentuk bilangan maka penyebutnya harus diusahakan menjadi bilangan bulat. Caranya dengan mengalikan penyebut tersebut dengan bentuk akar sekawannya.
Apa itu bentuk akar sekawan?
Bagaimana merasionalkan pecahan bentuk akar?

Klik materinya dibawah ini
Merasionalkan Pecahan Bentuk Akar

Cara Cepat Mengurutkan Berbagai Bilangan Pecahan

Dalam kesempatan ini akan kami berikan cara mengurutkan bilangan pecahan dari yang terkecil atau dari yang terbesar. Materi ini adalah materi yang sering keluar dalam ujian sekolah SD/MI. Nah, ternyata dari hasil survei soal tentang ini banyak yang masih ssalah dalam mengerjakan.
Ini contoh soal mengurutkan pecahan di Ujian Sekolah.

Prinsip dasar ketika kamu mengurutkan berbagai pecahan adalah kamu bisa mengubah berbagai pecahan menjadi bentuk desimal. Kenapa desimal? Karena mengurutkan pecahan dalam bentuk desimal lebih mudah.

Bagaimana membandingkan pecahan desimal?
Begini caranya.
Misalkan kita membandingkan bilangan 0,667 ; 0,29 ; 0,243 ; 1,021 

Cara membandingkan:
Pastikan tanda koma desimal lurus (sejajar)
Bandingkan urut dari depan (1 adalah bilangan paling besar dibandingkan dengan 0), berarti 1,021 paling besar.
Bandingkan angka yang menempati letak sepersepuluhan. (6 adalah angka paling besar dibanding dengan 2), berarti 0,662 menenpati urutan kedua terbesar.
Selanjutnya bandingkan pada angka yang terletak pada tempat seperseratusan, (9 lebih besar dibanding dengan 4), berarti 0,29 > 0,042.
Dari hasil membadingkan di atas diperoleh urutan bilangan dari yang terbesar/terkecil sebagai berikut.
1,021 ; 0,667 ; 0,29 ; 0,243  (urutan dari yang terbesar)
dan 
0,243 ; 0,29 ; 0,667 ; 1,021  (urutan dari yang terkecil) 

Nah, itu contoh cara mengurutkan bilangan pecahan desimal dari yang terkecil atau dari yang terbesar.

Selanjutnya kita akan mengurutkan berbagai bentuk pecahan dan cara menyelesaikannya. Mari perhatikan beberapa contoh berikut agar lebih mudah memahami cara menyelesaikannya.

 Coba perhatikan lagi

 Demikian cara mengurutkan berbagai pecahan yang dapat kami sampaikan.
Nah, sekarang cobalah menyelesaikan soal USM di atas. 
Pilihan mana yang benar?

Materi Terkait


Menyederhanakan Pecahan

Menjumlah dan Mengurangkan Pecahan

Cara Menyederhanakan Pecahan dan Mengubah Pecahan

Dalam kesempatan ini akan kami berikan materi tentang bilangan pecahan. Khususnya dalam hal menyederhanakan pecahan dan mengubah pecahan ke bentuk lain. Nah, menyederhanakan pecahan merupakan dasar untuk mempelajari tingkatan berikutnya. Jika kamu sudah mempelajari cara menyederhanakan pecahan, selanjutnya kamu akan mempelajari cara mengubah berbagai bentuk pecahan.Kali ini akanberikan secara singkat bagaimana cara menyederhanakan pecahan dan mengubah pecahan ke berbagai jenis pecahan.

1. Menyederhanakan pecahan
Dalam hal ini kita akan menyederhanakan bentuk pecahan biasa atau pecahan campuran. Kita tahu bahwa pecahan ada dua, yaitu pecahan sejati (pembilang lebih kecil daripada penyebut) dan pecahan tidak sejati (pembilang lebih dari penyebut)
 

Mari menyederhanakan Pecahan.
Cara menyederhanakan pecahan adalah membagi pembilang dan penyebut dengan FPB dari kedua bilangan tersebut.
Perhatikan beberapa contoh menyederhanakan pecahan berikut.

Oke, sudah jelas?
Sekarang sederhanakan pecahan - pecahan berikut.

2. Mengubah Pecahan
Bentuk/jenis Pecahan terdiri atas pecahan biasa/campuran, pecahan desimal, dan persen. Nah,dalam kesempatan ini kita akan belajar cara mengubah bentuk pecahan. Antara lain:
a. Mengubah pecahan biasa/campuran ke bentuk desimal
b. Mengubah pecahan biasa/campuran ke bentuk persen.
c. Mengubah pecahan desimal ke bentuk pecahan biasa/campuran.
d. Mengubah pecahan desimal ke bentuk persen.
e. Mengubah bentuk persen ke desimal.
f. Mengubah bentuk persen ke pecahan biasa.

Mari kita bahas satu per satu.
a. Mengubah pecahan biasa/campuran ke bentuk desimal
Cara:
Ubahlah pecahan biasa tersebut menjadi pecahan berpenyebut 10, 100 1.000, 10.000, dst. Dari pecahan tersebut ubahlah menjadi bentuk desimal.
Contoh:
 

 

b. Mengubah pecahan biasa/campuran ke bentuk persen
Persen adalah nama lain dari perseratus ( 1/100). Jadi, jika ada bilangan 5/100 sama artinya dengan 5%.

Cara:
Ubahlah pecahan biasa tersebut menjadi pecahan berpenyebut 100. Kemudian, ubahlah menjadi bentuk persen (%).
Contoh:

c. Mengubah pecahan desimal ke bentuk pecahan biasa/campuran
Cara:
Ubahlah pecahan biasa tersebut menjadi pecahan berpenyebut 10, 100 1.000, 10.000, dst. Dari pecahan tersebut kemudian sederhanakan.
Contoh:
 

d. Mengubah pecahan desimal ke bentuk persen
Ingat lagi bahwa persen adalah pecahan berpenyebut 100.
Berikut cara mengubah bentuk pecahan desimal menjadi pacahan bentuk persen.
Cara:
Ubahlah pecahan desimal menjadi pecahan biasa (berpenyebut 10, 100, 1.000, dst). Kemudian ubahlah pecahan tersebut menjadi pecahan berpenyebut 100. Baru, kemudian dijadikan bentuk persen (%).
Contoh:

e. Mengubah persen ke pecahan desimal
Ingat lagi bahwa persen adalah pecahan berpenyebut 100.
Pecahan berpenyebut 100 lebih mudah dijadikan bentuk desimal.
Berikut cara mengubah bentuk pecahan desimal menjadi pacahan bentuk persen.
Contoh:

f. Mengubah persen ke pecahan biasa
Ingat lagi bahwa persen adalah pecahan berpenyebut 100.
Cara  mengubah persen ke pecahan biasa
Ubahlah bentuk persen ke pecahanberpenyebut 100. Setelah itu, sederhanakan pecahan tersebut.

Contoh:

 Demikian sedikit pembelajaran tentang cara menyederhanakan pecahan dan cara mengubah berbagai bentuk pecahan.
Semoga bermanfaat.

Materi Terkait
Mengurutkan Pecahan

Menjumlah dan Mengurangkan Pecahan

Himpunan dan Operasi pada Himpunan

A. Himpunan

Himpunan adalah sekelompok/sekumpulan objek yang memiliki ciri, identitas, sifat, atau karakter yang sudah jelas/pasti.

Cara menyatakan himpunan:

1. Mendaftarkan semua anggotanya (metode enumerasi/tabulasi)

Contoh:

a.       A = {1, 3, 5, 7}

b.       B = {a, e, i, o, u}

2. Menyatakan sifat yang dimiliki anggotanya (metode deskripsi)

Contoh:

a.       A = himpunan bilangan ganjil kurang dari 8

b.       B = himpunan huruf vokal dalam huruf abjad

3. Menuliskan notasi pembentuk himpunan (metode bersyarat).

Contoh:

a.       A = {x, x < 8 x bilangan ganjil}

b.       B = {y, y merupakan huruf vokal}

B. Himpunan Semesta dan Himpunan Bagian

Himpunan semesta adalah himpunan yang memuat seluruh objek atau anggota himpunan yang dibicarakan. Himpunan semesta disimbolkan dengan S.

Himpunan A dikatakan himpunan bagian dari himpunan B yang disimbolkan dengan A ⊂B jika semua anggota A juga menjadi anggota B.

Jika banyaknya anggota suatu himpunan adalah n maka banyaknya himpunan bagian dari himpunan itu adalah 2ⁿ.

Contoh:

A = {1, 3, 5, 7, 9}

Himpunan semesta dari A antara lain:

S = { Himpunan bilangan ganjil}

S = { Himpunan bilangan asli kurang dari 10}

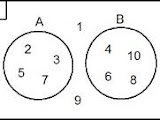
C. Diagram Venn

Diagram Venn merupakan bentuk lain dari penyajian suatu himpunan dengan cara menggunakan gambar. Adapun semua anggota dari himpunan semesta ditunjukan dengan noktah atau titik dalam suatu gambar persegi panjang. Adapun ketentuan dalam membuat diagram venn dalam adalah sebagai berikut :

1.  Himpunan semesta dinyatakan dalam persegi panjang. Simbol S untuk semesta disimpan di pojok kiri atas.

2.  Setiap himpunan yang dibicarakan selain (himpunan kosong)digambarkan dengan kurva tertutup.

3.  Setiap anggota ditunjukan dengan noktah (titik).

4.  Jika anggotanya sangat banyak maka cukup ditulis himpunannya saja

S = { 1, 2, 3, 4, 5, 6, 7 , 8, 9, 10}

A = { 2, 3, 5, 7}

B = {4, 6, 8, 10}

A dan B merupakan himpunan bagian dari S.

C. Komplemen Himpunan

Misalkan A suatu himpunan. Komplemen dari A adalah himpunan yang anggotanya bukan anggota himpunan A. Komplemen A disimbolkan A′ atau A^C.

A′ atau A^C dibaca komplemen himpunan A.

A′= {x | x ∉A}

Jika A merupakan himpunan bagian dari S (semesta), maka A^C dapat digambarkan sebagai berikut.

D. Operasi pada Himpunan

Irisan himpunan A dan B adalah himpunan yang anggotanya menjadi anggota A dan menjadi anggota B.

A n B dibaca irisan himpunan A dan B.

Diagram Venn

Gabungan himpunan A dan B adalah himpunan yang anggotanya merupakan anggota A atau anggota B.

A u B dibaca gabungan himpunan A dan B.

Diagram Venn.

 

 

Selisih (difference) himpunan A dan B adalah himpunan yang anggotanya semua anggota dari A, tetapi bukan anggota dari B. Dalam notasi himpunan dapat dituliskan:

Diagram Venn

Jika dalam operasi himpunan terdapat himpunan A dan B dengan masing-masing himpunan memiliki anggota sebanyak n(A) dan n(B), diperoleh hubungan berikut.

Contoh Soal dan Pembahasan


1. Perhatikan kumpulan/kelompok objek berikut. Kemudian, tunjukkan manakah yang merupakan himpunan atau tidak.
a. kumpulan siswa kelas VII SMP Negeri 1 Karanganyar.
b. Kumpulan siswa berbadan besar.
c. Komunitas mahasiswa pecinta  alam.
d. Kelompok pedagang kaki lima di kecamatan Waru.
e. Kelompok siswa yang pandai Matematika.

Jawaban:
a.  Kumpulan siswa di atas termasuk himpunan, sebab kriteria dan ciri yang masuk dalam kelompok tersebut sangat  jelas.  

 b.  Kumpulan siswa di atas bukan himpunan, sebab kriteria dan ciri siswa  relatif (belum ada batasannya). Berbadan besar itu bukan ukuran yang pasti.

  c.  Kumpulan mahasiswa di atas termasuk himpunan, sebab kriteria dan ciri siswa sangat jelas, yaitu mahasiswa pecinta alam (Mapala). Selain angota Mapala tidak masuk anggota.

   d.  Kumpulan pedagang kaki lima di atas termasuk himpunan, sebab kriteria dan ciri siswa sangat jelas, yaitu pedagang kaki lima. Selain angota Pedagag kaki lima dilarang masuk anggota.
   

 e.  Kumpulan siswa di atas bukan himpunan, sebab kriteria dan ciri siswa yang pandai itu relatif (belum ada batasannya).


2.  Tentukan himpunan semesta dari himpunan-himpunan berikut.
a. P = {sapi, kambing, kerbau, kuda}
b. Q = {2, 4, 6, 8, 10, 12}
c.  T = {trapesium, jajargenjang, persegi, persegi panjang, layang-layang, belah ketupat}

Jawaban :
a. S = {hewan berkaki empat}      
    S = {hewan pemakan rumput/tumbuhan)
    S = {hewan yang menghasilkan daging}
b. S = { bilangan genap kurang dari 20}
    S = { bilangan kelipatan dua}
    S = {bilangan faktor dari 120}
c.  S = {bangun datar segi empat}
    S = {bangun datar yang mempunyai 4 sisi}

3.     Diketahui himpunan S = {Bilangan Asli kurang dari 20}. Himpunan P, Q dan R merupakan himpunan bagian dari S. P = {Bilangan kelipatan 2 kurang dari 20}, Q = {Bilangan  kelipatan 3 kurang dari 20} dan R = {faktor dari 24}.
Tentukan:
a. Nyatakan P, Q, dan R dengan dengan mendata anggotanya.
b. P u Q (P gabungan Q)
c. P u R (P gabungan R)
d. P n Q (P irisan Q)
e. Q n R  (Q irisan R)
f.  P n Q n R 
g. P u Q u R
h. P u Q n R
i. P - Q
j. Q - P
k. (P - R)'  (' = komplemen)

Jawaban :
a. Langkah pertama kita tentukan dahulu anggota setiap himpunan dengan cara mendata anggotanya.
S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19}
P =  {2, 4, 6, 8, 10, 12, 14, 16, 18}
Q = {3, 6, 9, 12, 15, 18}
R = {1, 2, 3, 4, 6, 8, 12}

b. P u Q (Tulislah semua anggota baik di dalam himpunan P maupun Q)
    P u Q = {2, 3, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18}

c. P u R (Tulislah semua anggota himpunan P dan himpunan R)
    P u R = {1, 2, 3, 4, 6, 8, 10, 12, 14, 16, 18}

d. P n Q ( Tulislah semua anggota himpunan yang dimiliki P dan juga dimiliki Q)
    P n Q = {6, 12, 18}

e. Q n R (Tulislah semua anggota yang dimiliki oleh Q dan juga dimiliki R)
    Q n R = {3, 6, 12}

f. P n Q n R = (P n Q) n R
                  = {6, 12, 18} n {1, 2, 3, 4, 6, 8, 12}
                  = {6, 12}

g. P u Q u R = (P u Q) u R
                  = {2, 3, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18} u {1, 2, 3, 4, 6, 8, 12}
                  = {1, 2, 3, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18}

h.  P u Q n R = (P u Q) n R
                   =  {2, 3, 4, 6, 8, 9, 10, 12, 14, 15, 16, 18} n {1, 2, 3, 4, 6, 8, 12}
                   = {2, 3, 4, 6, 8, 12}

i. P -  Q (Tulislah semua anggota himpunan P yang bukan anggota Q}
   P - Q  = {2, 4, 6, 8, 10, 12, 14, 16, 18} - {3, 6, 9, 12, 15, 18}
            =  {2, 4, 8, 10, 14, 16}
 
j. Q - P (Tulislah semua anggota himpunan Q yang bukan anggota P}
   Q - P = {3, 6, 9, 12, 15, 18} - {2, 4, 6, 8, 10, 12, 14, 16, 18}
           = {3, 9, 15}

k.  (P - R)' (Tulislah semua anggota selain dari (P - R))
    Kita tentukan dahulu anggota P - R
   P - R = {2, 4, 6, 8, 10, 12, 14, 16, 18} - {1, 2, 3, 4, 6, 8, 12}
           = {14, 16, 18}
  (P - R)' = Himpunan yang anggotanya  selain anggota P - R
              = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19}- {14, 16, 18}
              = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 15, 17, 19}

4.

   Dari 40 orang anggota karang taruna, 21 orang gemar tenis meja, 27 orang gemar bulutangkis, dan 15 orang gemar tenis meja dan bulu tangkis. Banyak anggota karang taruna yang tidak gemar tenis meja maupun bulu tangkis adalah . . . .

A. 6 orang

B. 7 orang

C. 12 orang

D. 15 orang

Jawaban:

Misalkan:

M = {orang yang gemar tenis meja}

P = {orang yang gemar bulu tangkis}

     M n P =  {orang yang gemar tenis meja dan bulu tangkis}

    (M u P)^c = {orang yang tidak gemar tenis meja maupun bulu tangkis}

n(S) = 40

n(M) = 21

n(P) = 27

n(M n P) = 15

n(M u P)^c =x

n(S) = n(M) + n(P) - n(M n P) + n(M u P)^c

40 = 21 + 27 - 15 + x
40 =  33 + x
  x = 7
Jadi, banyak orang yang tidak gemar tenis meja maupun bulu tangkis adalah 7 orang.