Dalam kesempatan ini kita akan membahas dan belajar tentang Faktor prima, faktorisasi prima, Kelipatan persekutuan terkecil (KPK) dan Faktor persekutuan terbesar (FPB) menggunakan faktorisasi prima.
Faktorisasi Prima dan Faktor Prima
Bagilah dengan bilangan prima terkecil/termudah
Pilihlah pembagi yang bisa membagi kedua bilangan
Bagilah sampai selesai, hasilnya 1-1
KPK = 24 x 3 x 5 = 240
Tentukan KPK dari 45, 60, dan 75
45 = 3 x 3 x 5 = 32 x 5
60 = 2 x 2 x 3 x 5 = 22 x 3 x 5
75 = 3 x 5 x 5 = 3 x 52
KPK = 22 x 32 x 52 = 900
Demikian sedikit penjelasan tentang faktorisasi prima, faktor prima, KPK dan FPB.
Semoga bermanfaat.
Untuk mempelajari permasalahan dan penyelesaian masalah keseharian menggunakan KPK dan FPB, lanjutkan dengan KLIK di bawah ini.
Penyelesaian Permasalahan tentang KPK dan FPB
Faktorisasi Prima dan Faktor Prima
Bilangan prima adalah bilangan yang tepat mempunyai dua faktor yaitu 1 dan bilangan itu sendiri.
Bilangan prima = 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, . . . .
Faktorisasi prima adalah penjabaran suatu bilangan menjadi perkalian-perkalian bilangan prima. Jadi, dengan perkalian beberapa bilangan prima diperoleh hasil boilangan itu.
Contoh
6 = 2 x 3 (2 dan 3 adalah bilangan prima)
20 = 2 x 2 x 5 (2 dan 5 adalah bilangan prima)
45 = 3 x 3 x 5 (3 dan 5 adalah bilangan prima)
70 = 2 x 5 x 7 (2, 5, dan 7 adalah bilangan prima)
Bentuk bentuk di atas merupakan contoh faktorisasi prima dari suatu bilangan.
Faktor Prima adalah bilangan-bilangan prima yang terdapat pada faktorisasi prima.
Misalkan pada faktorisasi prima di atas.
6 memiliki faktor prima 2 dan 3 .
20 memiliki faktor prima 2 dan 5.
45 memiliki faktor prima 3 dan 5.
70 memiliki faktor prima 2, 3, dan 5.
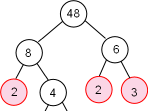
Untuk bilangan-bilangan yang kecil, mungkin mudah untuk membuat faktorisasi prima. Namun untuk bilangan yang besar perlu pemikiran yang lebih. Pada kesempatan ini mari membuat faktorisasi bilangan yang lebih besar. Caranya dengan pohon faktor. Prinsip pohon faktor adalah pembagian bilangan sampai dengan bilangan prima pada ujung-ujungnya.
Perhatikan cara berikut.
Faktorisasi prima dari 48
48 = 2 x 2 x 2x 2 x 3 = 24 x 3
Faktor prima = 2 dan 3
Faktorisasi prima dari 90
90 = 2 x 3 x 3 x 5 = 2 x 32 x5
Faktor prima = 2, 3 dan 5
Faktorisasi prima dari 140
140 = 2 x 2 x 5 x 7 = 22 x 5 x 7
Faktor prima = 2, 5 dan 7
Faktorisasi prima dari 240
240 = 2 x 2 x 2 x 2 x 3 x 5 = 24 x 3 x 5
Faktor prima = 2, 3 dan 5
Menentukan FPB menggunakan Faktorisasi Prima
Langkah-langkah menentukan FPB
1. Tulislah semua faktorisasi prima dari setiap bilangan
2. Pilihlah bilangan faktor yang sama dan kalikanlah
3. Pada bilangan faktor yang ada pangkatnya, pilihlah bilangan dengan pangkat terkecil
Contoh:
Tentukan FPB dari 60 dan 36
60 = 2 x 2 x 3 x 5 = 22 x 3 x 5
36 = 2 x 2 x 3 x 3 = 22 x 32
FPB = 22 x 3 = 12 (pada bilangan 3 dipilih pangkat terkecil yaitu 3)
Cara kedua
Bagilah dengan bilangan prima terkecil/termudah
Pilihlah pembagi yang bisa membagi kedua bilangan
FPB = 2 x 2 x 3 = 12
Tentukan FPB dari 120 dan 300
120 = 2 x 2 x 2 x 3 x 5 = 23 x 3 x 5
300 = 2 x 2 x 3 x 5 x 5 = 22 x 3 x 52
FPB = 22 x 3 x 5 = 60 (pada bilangan 2 dan 5 dipilih pangkat terkecil yaitu 22 dan 5)
Cara Kedua
Bagilah dengan bilangan prima terkecil/termudah
Pilihlah pembagi yang bisa membagi kedua bilangan
FPB = 22 x 3 x 5 = 60
Menentukan KPK menggunakan Faktorisasi Prima
Langkah-langkah menentukan FPB
1. Tulislah semua faktorisasi prima dari setiap bilangan
2. Tulislah semua bilangan faktor yang sama
3. Jika ada bilangan faktor yang berpangkat, pilihlah bilangan dengan pangkat terbesar, kemudian kalikanlah
Contoh:
Tentukan KPK dari 30 dan 48
30 = 2 x 3 x 5
48 = 2 x 2 x 2 x 2 x 3 = 24 x 3
Faktor Prima adalah bilangan-bilangan prima yang terdapat pada faktorisasi prima.
Misalkan pada faktorisasi prima di atas.
6 memiliki faktor prima 2 dan 3 .
20 memiliki faktor prima 2 dan 5.
45 memiliki faktor prima 3 dan 5.
70 memiliki faktor prima 2, 3, dan 5.
Untuk bilangan-bilangan yang kecil, mungkin mudah untuk membuat faktorisasi prima. Namun untuk bilangan yang besar perlu pemikiran yang lebih. Pada kesempatan ini mari membuat faktorisasi bilangan yang lebih besar. Caranya dengan pohon faktor. Prinsip pohon faktor adalah pembagian bilangan sampai dengan bilangan prima pada ujung-ujungnya.
Perhatikan cara berikut.
Faktorisasi prima dari 48
48 = 2 x 2 x 2x 2 x 3 = 24 x 3
Faktor prima = 2 dan 3
Faktorisasi prima dari 90
90 = 2 x 3 x 3 x 5 = 2 x 32 x5
Faktor prima = 2, 3 dan 5
Faktorisasi prima dari 140
140 = 2 x 2 x 5 x 7 = 22 x 5 x 7
Faktor prima = 2, 5 dan 7
Faktorisasi prima dari 240
240 = 2 x 2 x 2 x 2 x 3 x 5 = 24 x 3 x 5
Faktor prima = 2, 3 dan 5
Menentukan FPB menggunakan Faktorisasi Prima
Langkah-langkah menentukan FPB
1. Tulislah semua faktorisasi prima dari setiap bilangan
2. Pilihlah bilangan faktor yang sama dan kalikanlah
3. Pada bilangan faktor yang ada pangkatnya, pilihlah bilangan dengan pangkat terkecil
Contoh:
Tentukan FPB dari 60 dan 36
60 = 2 x 2 x 3 x 5 = 22 x 3 x 5
36 = 2 x 2 x 3 x 3 = 22 x 32
FPB = 22 x 3 = 12 (pada bilangan 3 dipilih pangkat terkecil yaitu 3)
Cara kedua
Bagilah dengan bilangan prima terkecil/termudah
Pilihlah pembagi yang bisa membagi kedua bilangan
FPB = 2 x 2 x 3 = 12
Tentukan FPB dari 120 dan 300
120 = 2 x 2 x 2 x 3 x 5 = 23 x 3 x 5
300 = 2 x 2 x 3 x 5 x 5 = 22 x 3 x 52
FPB = 22 x 3 x 5 = 60 (pada bilangan 2 dan 5 dipilih pangkat terkecil yaitu 22 dan 5)
Cara Kedua
Bagilah dengan bilangan prima terkecil/termudah
Pilihlah pembagi yang bisa membagi kedua bilangan
FPB = 22 x 3 x 5 = 60
Menentukan KPK menggunakan Faktorisasi Prima
Langkah-langkah menentukan FPB
1. Tulislah semua faktorisasi prima dari setiap bilangan
2. Tulislah semua bilangan faktor yang sama
3. Jika ada bilangan faktor yang berpangkat, pilihlah bilangan dengan pangkat terbesar, kemudian kalikanlah
Contoh:
Tentukan KPK dari 30 dan 48
30 = 2 x 3 x 5
48 = 2 x 2 x 2 x 2 x 3 = 24 x 3
KPK = 24 x 3 x 5 = 240 (pada bilangan 2 dipilih pangkat terbesar yaitu 24 )
Cara kedua
Bagilah dengan bilangan prima terkecil/termudah
Pilihlah pembagi yang bisa membagi kedua bilangan
Bagilah sampai selesai, hasilnya 1-1
KPK = 24 x 3 x 5 = 240
Tentukan KPK dari 45, 60, dan 75
45 = 3 x 3 x 5 = 32 x 5
60 = 2 x 2 x 3 x 5 = 22 x 3 x 5
75 = 3 x 5 x 5 = 3 x 52
KPK = 22 x 32 x 52 = 900 (pada bilangan 2, 3, dan 5 dipilih pangkat terbesar)
Cara kedua
KPK = 22 x 32 x 52 = 900
Demikian sedikit penjelasan tentang faktorisasi prima, faktor prima, KPK dan FPB.
Semoga bermanfaat.
Untuk mempelajari permasalahan dan penyelesaian masalah keseharian menggunakan KPK dan FPB, lanjutkan dengan KLIK di bawah ini.
Penyelesaian Permasalahan tentang KPK dan FPB