Rumah Rumus Pelajaran

Menentukan Volume dan Luas Permukaan Bangun Ruang Sisi Datar (Kubus, Balok, Prisma dan Limas)

Pada Kesempatan ini akan saya berikan mteri tentang bangun ruang yang berkaitan dengan volume, luas permukaan dan unsur-unsur di dalamnya.

Dalam kesempatan ini akan membahas antara lain volume dan luas permukaan kubus, balok, prisma, dan limas, serta gabungan dari bangun-bangun terseebut.

Ini adalah materi pelajaran SMP. Perlu diingat bahwa langkah penyelesaian dalam materi ini kadang-kadang menggunakan konsep Rumus Pythagoras juga. Sebab dengan konsep itu maka unur-unsur seperti rusuk dapat ditentukan panjangnya.

Satu hal lagi yang kamu perhatikan adalah penguasaan rumus-rumus dasar bangun ruang (Volume dan luas permukaan) harus benar-benar anda hafal diluar kepala.

Perhatikan beberapa contoh berikut.

1. Sebuah balok berukuran panjang 12 cm, lebar 9 cm, dan tinggi 8 cm.

Tentukan:

a. Volume balok

b. Luas permukaan balok

c. Panjang diagonal ruang

Jawaban :

Diketahui p = 12 cm, l = 9 cm, dan t = 8 cm.

a. Volume = p x l x t

= 12 x 9 x 8

= 864

Jadi, volume balok adalah 864 cm kubik.

b. Luas Permukaan = 2 (pl + lt + pt)

= 2 x (12 . 9 + 9 . 8 + 12 . 8)

= 2 x (108 + 72 + 96)

= 2 x 276

= 552

Jadi, luas permukaannya adalah 552 cm persegi.

c. Diagonal ruang

Jadi, Panjang diagonal ruang balok adalah 17 cm.

2. Diketahui kubus dengan panjang rusuk 12 cm.

Tentukan volume, luas permukaan, panjang diagonal ruang, dan luas bidang diagonal.

Jawaban :

Volume = s x s x s

= 12 x 12 x 12

= 1.728

Jadi, volume kubus adalah 1.728 cm kubik.

Luas permukan = 6 x s x s

= 6 x 12 x 12

= 864

Jadi, luas permukaan kubus adalah 864 cm persegi

Panjang diagonal ruang (CE) = 12V3 cm (V = simbol akar)

Luas bidang diagonal (ABGH) = s x sV2

= 12 x 12V2

= 144V2 cm persegi

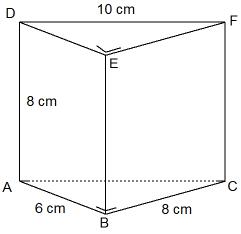
3. Perhatikan prisma segitiga berikut.

Tentukan volume dan luas permukaan prisma segitiga tersebut.

Jawaban :

Luas permukaan = 2 x Luas alas + Luas selimut

Luas alas = 1/2 x AB x BC

= 1/2 x 6 x 8

= 24 cm2

Luas Selimut = Keliling alas x tinggi

= (AB + BC + A) x AD

= (6 + 8 + 10) x 8

= 24 x 8

= 192 cm2

Jadi diperoleh luas permukaan prisma sebagai berikut

L = (2 x 24) + 192

= 48 + 192

= 240 cm2

Volume = Luas alas x tinggi

= 24 x 8

= 192 cm3

4. Perhatikan limas segi empat beraturan berikut.

Tentukan Volume dan luas permukaan limas tersebut.

Jawaban :

Volume = 1/3 x Luasalas x Tinggi

= 1/3 x (AB x BC) x OT

= 1/3 x 10 x 10 x 12

= 400 cm3

Luas Permukaan = Luas alas + Luas selimut

= 400 + (4 x 1/2 x BC x TE)

= 400 + (2 x 10 x 13)

= 400 + 260

= 460 cm2

Demikian sedikit tentang cara menghitung luas permukaan dan volume bangun ruang sisi datar.

Semoga bermanfaat.

Menyelesaikan dan Menentukan Nilai Integral Tentu

Beberapa materi mapel Matematika SMA yang agak sulit adalah materi Integral. Integral merupakan kebalikan dari turunan fungsi (diferensial). Yang akan kita pelajari di sini adalah integral tentu dan integral taktentu dari fungsi aljabar.

Jika kita mempunyi fungsi y = f(x) maka turunannya adalah y' = dy/dx, atau y' = f'(x). Sehingga integral dari y' adalah y, atau integral dari dy/dx adalah y.

Setelah mempelajari integral tak tentu di postingan yang lalu, selanjutnya akan kami berikan cara menentukan hasil integral tentu. Integral tentu yaitu suatu integral fungsi yang memiliki batas atas dan batas bawah untuk disubstitusikan pada hasil pengintegralan.

Jika integral dari f(x) adalah F(x), maka :