Segitiga-segitiga yang Sebangun – Apabila di dalam pembahasan materi sebelumnya kita telah mempelajari mengenai kesebangunan pada bangun datar, maka pada pembahasan kali ini kita akan lebih fokus di dalam membahas materi tentang kesebangunan pada segitiga. Di sini Rumus Matematika Dasar akan menjelaskan syarat dari segitiga-segitiga yang sebangun serta aplikasinya. Oleh karenanya, simak dengan baik pembahasan yang ada di bawah ini:
Syarat Segitiga-Segitiga yang Sebangun
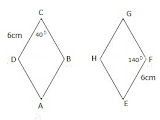
Coba kalian amati dengan baik kedua gambar segitiga di bawah ini:
Pada segitiga ABC dan DEF di atas, perbandingan antara sisi-sisi yang bersesuaian pada kedua segitiga tersebut dapat diuraikan menjadi sebagai berikut:
DE/AB= 4/8 = 1/2
EF/BC = 3/6 = 1/2
DF/AC = 5/10 = 1/2
Dengan demikian, dapat disimpulkan bahwa AB/DE = BC/EF = AC/DF = 1/2
Apabila kalian melakukan pengukuran pada sudut-sudut yang bersesuaian pada kedua segitiga tersebut maka kalian akan menemukan bahwa sudut A = sudut D, sudut B = sudut E, dan sudut C = sudut F.
Jadi, kesebangunan dari dua buah segitiga dapat kita ketahui dengan mencari atau membuktikan bahwa perbandingan antara panjang sisi-sisi yang bersesuaian memiliki nilai yang sama.
Sekarang coba perhatikan gambar segitiga siku-siku yang ada di bawah ini:
Pada segitiga siku-siku ABC dan DEF di atas, kita dapat melihat bahwa sudut A = sudut D yaitu 900
Sedangkan sudut B = sudut E yaitu 600. Oleh karenanya, kita dapat menghitung sudut C dan sudut F dengan melakukan perhitungan:
Sudut C = sudut F = 1800– 900 - 600 = 300
Jika kalian melakukan pengukuran terhadap panjang sisi-sisi yang ada pada kedua segitiga tersebut, maka hasil perbandingannya akan menjadi:
AB/DE = BC/EF = AC/DF
Karena pada segitiga siku-siku ABC dan DEF panjang sisi-sisi yang bersesuaian memiliki nilai yang sama dan sudut-sudut yang bersesuaiannya juga memiliki ukuran yang sama besar maka dapat disimpulkan bahwa segitiga ABC sebangun dengan segitiga DEF.
Maka, dapat kita simpulkan bahwa kesebangunan dari dua buah segitiga dapat diketahui dengan cara menunjukkan bahwa sudut-sudut yang bersesuaian diantara dua buah segitiga tersebut memiliki nilai yang sama besar. Sehingga, syarat agar dua buah segitiga dapat dikatakan sebangun adalah:
1. Perbandingan panjang sisi yang bersesuaian senilai
2. Dua pasang sudut yang bersesuaian sama besar.
Demikianlah penjelasan materi tentang Segitiga-segitiga yang Sebangun dan syarat-syarat yang harus dipenuhi agar dua buah segitiga dapat dikatakan sebangun. Semoga kalian dapat memahaminya dengan baik, dan apabila ada kesulitan di dalam memahami penjelasan di atas kalian bisa menanyakannya pada orang tua ataupun guru di sekolah. Atau kalian juga boleh menyampaikannya pada kolom komentar yang ada di bawah postingan ini. Sampai jumpa lagi pada pmbahasan materi pelajaran matematika selanjutnya.
Simak juga artikel tentang Segitiga-segitiga yang Kongruen
Source: Salamah. U. 2012. Berlogika Dengan Matematika 3. Solo : Platinum