Pengertian Persamaan Garis Lurus dan Cara Menggambarnya

Pengertian Persamaan Garis Lurus - Persamaan garis lurus juga dapat disebut sebagai persamaan linear. persamaan linear ada yang terdiri dari satu variabel dan ada juga yang terdiri dari dua variabel. Karena Rumus Matematika Dasar sudah pernah memberikan penjelasan mengenai Persamaan Linear Satu Variabel dan Persamaan Linear Dua Variabel maka postingan kali ini akan difokuskan kepada pembahasan mengenai persamaan garis lurus dan langkah-langkah untuk menggambarnya. 

Pengertian dan Cara Menggambar Persamaan Garis Lurus

Secara sederhana persamaan garis lurus dapat didefinisikan sebagai sebuah garis lurus dimana posisinya ditentukan oleh sebuah persamaan dan apabila persamaan tersebut digambarkan pada bidang cartesius maka akan menghasilkan sebah garis yang lurus. Salah satu contoh persamaan yang menghasilkan garis lurus adalah x + y = 3. Bagaimana kita bisa mengetahui bahwa persamaan tersebut dapat menghasilkan garis lurus? mari langsung saja kita buktukan dengan cara berikut ini:

Salah satu cara yang bisa kita lakukan untuk membuktikan persamaan garis lurus adalah dengan menggambarkan garis lurus ke dalam bidang cartesius dengan menggunakan koordinat yang dihasilkan dari persamaan tersebut, contohnya:

Kita misalkan x = 0, maka:

x + y = 3

0 + y = 3

y = 3

titik pertama yang kita peroleh adalah koordinat (0, 3)

Kita misalkan x = 1, maka:

x + y = 3

1 + y = 3

y = 2

titik kedua yang kita peroleh adalah koordinat (1, 2)

Kita misalkan x = 2, maka:

x + y = 3

2 + y = 3

y = 1

titik ketiga yang kita peroleh adalah koordinat (2, 1)

Kita misalkan x = 3, maka:

x + y = 3

3 + y = 3

y = 0

titik kedua yang kita peroleh adalah koordinat (3, 0)

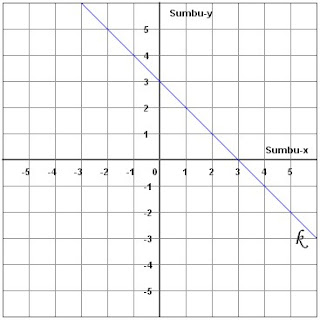
Setelah kita menemukan koodinatnya, tinggal kita masukkan saja ke dalam bidang cartesius, sehingga hasilnya menjadi seperti ini:

Dari gambar di atas kita dapat melihat bahwa ketika kita menarik garis diantara titik-titik koordinat yang diperoleh, maka akan dihasilkan sebuah garis yang lurus. Itu artinya kita dapat menyimpulkan bahwa persamaan x + y = 3 terbukti sebagai sebuah persamaan garis lurus.

Bagaimana? Apakah kalian sudah mengerti dan paham tentang pengertian persamaan garis lurus dan cara menggambarnya? Jika kalian mengamati penjelasan di atas dengan baik, tidaklah sulit untuk bisa memahami apa itu persamaan garis lurus serta bagaimana cara menggambarkannya ke dalam koordinat cartesius. Semoga penjelasan materi ini bermanfaat untuk kalian semua.

Pengertian Notasi Himpunan dan Anggota Himpunan

Notasi Himpunan dan Anggota Himpunan - Di dalam beberapa postingan sebelumnya Rumus Matematika Dasar pernah memberikan materi seputar Pengertian Himpunan. Untuk postingan kali ini materi yang dibahas masih berkaitan dengan pembahasan seputar himpunan yaitu pengertian notasi dan anggota himpunan. Kalian pastinya sudah mengetahui bahwa di dalam matematika biasanya suatu himpunan dinyatakan dengan menggunakan huruf kapital seperti A, B, C, D, E, F, ... dst. Adapun objek atau hal-hal lain yang terdapat di dalam himpunan tersebut dituliskan diantara kurung kurawal {....} dan tiap-tiap objek itu dipisahkan dengan menggunakan koma, contohnya adalah:

- A merupakan himpunan bilangan ganjil dari yang lebih kecil dari 15, 

   maka A = {1, 3, 5, 7, 9, 11, 13}

- B merupakan himpunan bilangan genap antara 1 dan 13 

   maka B = {2, 4, 6, 8, 10, 12}

Tiap-tiap objek ataupun benda yang berada di dalam kurung kurawal adalah anggota dari himpunan tersebut. Anggota himpunan biasa disebut juga sebagai elemen yang dinotasikan dengan lambang ∈. Sedangkan objek-objek ataupun benda yang tidak termasuk kedalam suatu himpunan dapat dianggap bukan anggota dari himpunan tersebut dan biasanya dinotasikan dengan lambang ∉.

Jumlah anggota dari suatu himpunan basanya dinyatakan sebagai n. Apabila C = {2, 3, 5, 6, 7, 8, 9, 11} maka banyaknya anggota himpunan B dituliskan sebagai n(C) = 8.

Di dalam matematika, himpunan bilangan tertentu biasanya dilambangkan atau dinotasikan dengan menggunakan huruf kapital tertentu, contohnya:

Contoh soal Notasi dan Anggota Himpunan

a. A adalah himpunan hewan laut.

b. K adalah hmpunan bilangan cacah yang kurang dari 10

c. M adalah himpunan nama bulan yang diawali dengan huruf J.

Jawab:

a. Anggota himpunan hewan laut adalah ikan, gurita, cumi-cumi, kerang, dst. Maka, A = {ikan, gurita, cumi-cumi, kerang,... dsb.}

b. Anggota himpunan bilangan cacah yang kurang dari 10 adalah 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Maka, K = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

c. Anggota himpunan nama bulan yang diawali dengan huruf J adalah Januari, Juni, dan Juli. Maka, M = {Januari, Juni, Juli}

Itulah sedikit penjelasan materi mengenai Pengertian Notasi Himpunan dan Anggota Himpunan. Semoga bermanfaat dan semoga kalian bisa menyerap materi tersebut dengan baik. Ikuti terus postingan Rumus Matematika Dasar untuk terus engasah kemampuan dan pengetahuan kalian mengenai pelajaran matematika. Sampai jumpa dan terima kasih.

Pengertian Gabungan Dua Himpunan dan Cara Menentukannya

Pengertian Gabungan Dua Himpunan - Ada cukup banyak materi yang berkaitan dengan himpunan diajarkan pada bangku sekolah menengah pertama. Salah satu diantaranya adalah mengenai gabungan dua himpunan. Tahukah kalian apa yang dimaksud sebagai gabungan dari dua himpunan? ada baiknya bila kalian membaca lagi materi Rumus Matematika Dasar yang membahas tentang Pengertian, Teori, Konsep Dan Jenis Himpunan Matematika jika kalian sudah memahami dengan baik apa itu yang disebut dengan himpunan maka kalian pastinya akan lebih mudah dalam memahami materi yang akan di bahas pada artikel ini. Sebelum kita beranjak lebih jauh ke dalam pembahasan materi, sebaiknya kalian amati terlebih dahulu contoh uraian berikut ini:

Pak Sukirlan pergi ke pasar untuk membeli beberapa jenis buah. Setelah berbelanja Pak Sukirlan kemudian pulang ke rumah dengan membawa dua buah keranjang. Keranjang pertama di isi dengan buah kelengkeng, duku, dan rambutan. Sementara keranjang yang kedua di isi dengan buah jambu, markisa, dan rambutan. Setibanya di rumah, buah-buahan tersebut di satukan ke dalam sebuah keranjang besar sehingga keranjang besar tersebut kini berisi gabungan buah-buahan yang dibeli oleh pak Sukirlan yaitu kelengkeng, duku, rambutan, jambu, dan markisa.

Dari contoh uraian di atas, kita dapat menyimpulkan bahwa apabila kedua keranjang yang dibawa oleh pak Sukirlan adalah himpunan A dan B. maka, gabungan dari himpunan A dan B adalah himpunan yang anggotanya merupakan anggota-anggota yang ada di himpunan A atau anggota-anggota yang ada di himpunan B. atau di dalam matematika dapat dituliskan menjadi:

A ∪ B = A union B (A gabungan B)

Cara Menentukan Gabungan Dua Himpunan

1. Himpunan Bagian

apabila A ⊂ C maka A ∪ B = B

Artinya, apabila anggota himpunan A termasuk ke dalam anggota himpunan B ( A adalah himpunan bagian dari B) maka gabungan dari kedua himpunan tersebut berisi seluruh anggota himpunan B.

2. Kedua Himpunan Beranggotakan Sama

apabila A = B maka A ∪ B = A = B

Artinya apabila anggota himpunan A sama persis dengan anggota himpunan B, maka gabungan dari kedua himpunan tersebut berisi anggota himpunan A atau B.

3. Himpunan tidak saling lepas

Sebagai contoh A = { 2, 3, 4, 6, 8} dan B = {2, 5, 6, 9} maka A U B = {2, 3, 4, 5, 6, 8, 9}

Banyaknya jumlah anggota dari gabungan dua himpunan dapat ditentukan dengan menggunakan rumus di bawah ini:

n(A ∪ B) = n(A) + n(B) - n(A ∩ B)

Contoh Soal:

Diketahui:

X = {1, 2, 3, 4, 6, 8}
Y = {2, 4, 5, 6, 9, 11}

Tentukanlah:

a.  anggota X ∩ Y
b. anggota X ∪ Y
c. n(X ∪ Y)


Jawab:

a. X ∩ Y = {2, 4, 6}
b. X ∪ Y = {1, 2, 3, 4, 5, 6, 8, 9, 11}
c. n(X ∪ Y)
n(X ∪ Y) = n(X) + n(Y) - n(X ∩ Y)
n(X ∪ Y) = 6 + 6 - 3
n(X ∪ Y) = 9


Sekian penjelasan dan contoh soal mengenai Pengertian Gabungan Dua Himpunan dan Cara Menentukannya semoga dapat membantu kalian untuk memahami lebih jauh materi mengenai himpunan. Sampai berjumpa pada pembahasan materi pelajaran matematika selanjutnya.

Cara Menghitung Banyaknya Himpunan Bagian dari Suatu Himpunan

Menghitung Banyaknya Himpunan Bagian - Rumus Matematika Dasar telah menjelaskan tentang Pengertian, Rumus Dan Contoh Himpunan Bagian. untuk menambah pengetahuan kalian mengenai materi tersebut, kali ini akan di bahas materi lanjutan tentang himounan bagian yaitu mengenai cara menentukan atau menghitung banyaknya himpunan bagian dari suatu himpunan. Sebagai langkah awal, coba kalian perhatikan gambar tabel di bawah ini:

Dari tabel tersebut kita dapat melihat bahwa ada sebuah hubungan antara jumlah anggota dari suatu himpunan dengan jumlah himpunan bagiannya. oleh karena itu, kita dapat menarik kesimpulan bahwa jumlah himpunan bagian dari suatu himpunan adalah 2n dimana n merupakan jumlah keseluruhan anggota dari himpunan tersebut.

Di dalam mencari dan menghitung banyaknya himpunan bagian yang mempunyai anggota sebanyak n, kita dapat menggunakan pola bilangan pada segitiga pascal seperti di bawah ini:

Jika kalian amati, pada pola blangan pascal di atas, bilangan yang berada di tengah merupakan hasil dari penjumlahan angka yang ada di atasnya. pola bilangan segitiga pascal tersebut dapat kita uraikan menjadi:

Himpunan bagian dari {a,b,c,d} yang memiliki anggota sebanyak 0 ada 1 :

{ }

Himpunan bagian dari {a,b,c,d} yang memiliki anggota sebanyak 1 ada 4 :

{a}, {b}, {c}, {d}

Himpunan bagian dari {a,b,c,d} yang memiliki anggota sebanyak 2 ada 6 :

{b,a}, {c,a}, {d,a}, {b,c}, {b,d}, {c,d}

Himpunan bagian dari {a,b,c,d} yang memiliki anggota sebanyak 3 ada 4 :

{a,b,c}, {b,c,d}, {c,d,a}, {d,a,b}

Himpunan bagian dari {a,b,c,d} yang memiliki anggota sebanyak 4 ada 1 :

{a,b,c,d}

Begitulah kiranya cara Menghitung Banyaknya Himpunan Bagian dari Suatu Himpunan yang bisa kalian coba lakukan. Semoga bisa mempermudah kalian dalam mengerjakan soal-soal yang berkaitan dengan materi himpunan.

Cara Menghitung Rumus Mencari Tinggi Jajar Genjang

Cara Mencari Tinggi Jajar Genjang - Di dalam pembahasan materi Rumus Matematika Dasar sebelumnya, telah dijelaskan mengenai Cara Menghitung Rumus Luas Dan Keliling Jajar Genjang Lengkap. Apabila kalian telah memahami materi tersebut dengan baik, tentu kalian akan bisa dengan mudah memahami materi yang akan di jelaskan di dalam artikel ini yaitu mengenai bagaimana cara mencari tinggi dari sebuah jajar genjang apabila telah diketahui luasnya.

Rumus Mencari Tinggi Jajar Genjang

Apabila kalian telah membaca artikel saya sebelumnya mengenai rumus luas dan keliling jajar genjang kalian akan mengerti bahwa untuk mengetahui luas dari sebuah jajar genjang kita dapat mengetahuinya dengan cara mengalikan tinggi dengan panjang alas dari jajar genjang tersebut. Mari kita lihat kembali rumus luas jajar genjang di bawah ini:

L = a x t

dengan sedikit memutar rumus tersebut maka kita bisa mencari tinggi dari sebuah jajar genjang yang telah diketahui luasnya. caranya adalah dengan membagi luas jajar genjang dengan panjang alas yang diketahui. bila dirumuskan maka akan menjadi seperti di bawah ini:

t = L/a

mari kita amati bersama bagaimana menggunakan rumus-rumus tersebut untuk menyelesaikan contoh soal seperti berikut ini:

Soal 1

diketahui luas dari sebuah jajar genjang adalah 150 cm2. apabila panjang alas dari jajar genjang tersebut adalah 30 cm, berapakah tingginya?

Penyelesaian:

Diketahui: 

Luas = 150 cm2

Panjang alas = 30 cm

Ditanyakan: t = ....?

Jawab:

L = a x t

t = L/a

t = 150/30

t = 5 cm

maka, tinggi dari jajar genjang itu adalah 5 cm.

Soal 2

Sebuah jajar genjang memiliki luas 2400 cm2. apabila tinggi dan panjang alas dari jajar genjang tersebut berturut-turut adalah 4x dan 6x, maka hitunglah:

a. nilai x

b. panjang alas dan tinggi sebenarnya dari jajar genjang itu

Penyelesaian:

Diketahui:

Luas = 2400 cm2

Panjang Alas = 6x

tinggi = 4x

Ditanyakan:

a. x = ....?

b. a = ....cm? dan t = ...cm?

Jawab:

L = a x t

2400 cm2 = 6x cm x 4x cm

2400 cm2 = 24x2 cm2

x2 = 2400/24

x2 = 100

x = 10

Panjang alas = 6x = 6 x 10 = 60 cm

Tinggi = 4x = 4 x 10 = 40 cm

Demikianlah pembahasan dan contoh soal mengenai Cara Menghitung Rumus Mencari Tinggi Jajar Genjang. Semoga kalian semua bisa memahaminya dengan baik. Mohon maaf apabila di dalam penyampaian materi ini terdapat kata-kata atau hasil perhitungan yang salah. Kami dengan senang hati selalu menerima kritik dan saran dari anda semua. Terima kasih dan sampai berjumpa lagi dalam materi-materi matematika selanjutnya.

Cara Menghitung Diskon Harga Suatu Produk

Cara Menghitung Diskon Harga Suatu Produk - Jika kalian bepergian ke supermarket ataupun mal pasti kalian pernah melihat angka-angka yang dipajang dengan kata-kata diskon 50%, diskon 30%, sale 20% dan sebagainya. Tahukah kalian bahwa tanda-tanda tersebut sebenarnya menyatakan potongan harga dari suatu produk atau biasa dikenal dengan sebutan diskon. Dengan adanya diskon kalian bisa membeli suatu produk dengan harga yang lebih murah daripada harga aslinya. Tentunya harga dari barang tersebut dipotong sesuai dengan diskon yang berlaku untuk barang itu. Tapi tahukah kalian bagaimana sebenarnya cara menghitung harga barang yang telah diberikan diskon? Jika kalian belum mengetahuinya, coba simak penjelasan Rumus Matematika Dasar di bawah ini tentang diskon atau potongan harga barang:

Cara Menghitung Harga Barang Setelah Diskon

Cara menghitung harga dari suatu barang yang dikenakan diskon sebenarnya tidaklah terlalu sulit, sebagai contoh apabila suatu barang memiliki harga Rp. 500.000, kemudian barang tersebut dikenakan diskon 25%, maka pertama-tama kita harus menghitung terlebih dahulu berapa jumlah diskon yang sebenarnya diberlakukan untuk barang itu.

Harga diskon = harga awal x persentase diskon

Harga diskon = Rp. 500.000 x 25%

Harga diskon = Rp. 500.000 x 25/100

Harga diskon = Rp. 125.000

Setelah mengetahui harga diskonnya, barulah kita bisa mengetahui potongan harga untuk barang tersebut. Maka, jumlah uang yang harus kita bayar untuk barang tersebut adalah:

Harga akhir = harga awal - harga diskon

Harga akhir = Rp. 500. 000 - Rp. 125.000

Harga akhir = Rp. 375.000

Jadi harga barang tersebut setelah dipotong diskon adalah Rp. 375.000

Bagaimana, sudah mengerti? Untuk lebih memahaminya perhatikan beberapa contoh soal dan cara penyelesaiannya di bawah ini:

Contoh Soal 1:

Budi ingin membeli sebuah tas ransel dengan harga Rp. 125.000 karena pada saat itu bertepatan dengan tahun baru, maka tas tersebut diberikan diskon sebanyak 30%. Maka, berapakah jumlah uang yang harus dikeluarkan oleh Budi untuk membeli tas ransel tersebut?

Penyelesaian:

Diketahui:

Harga awal = Rp. 125.000

Harga diskon = harga awal x persentase diskon

Harga diskon = Rp. 125.000 x 30%

Harga diskon = Rp. 125.000 x 30/100

Harga diskon = Rp. 37.500

Ditanyakan:

Harga akhir = ...?

Harga akhir = harga awal - harga diskon

Harga akhir = Rp.125.000 - Rp. 37.500

Harga akhir = Rp.87.500

Jadi jumlah uang yang harus dibayar Budi untuk membeli tas tersebut adalah Rp. 87.500

Contoh Soal 2:

Ibu Ani ingin membeli sebuah kulkas, setelah menemukan kulkas yang ia inginkan, Ibu ani pun pergi menuju kasir untuk membayar kulkas tersebut. Setelah diberikan potongan harga sebanyak 40% harga kulkas tersebut menjadi Rp. 750.000. Hitunglah berapa harga awal dari kulkas tersebut sebelum diberikan diskon.

Penyelesaian:

Diketahui:

Harga akhir = Rp. 750.000

persentase diskon = 40 %

Ditanyakan:

Harga awal = ...?

Gunakan Logika perbandingan :

X% +Y% = Z %
40% + 60 % = 100 %


Rp X + Rp 750,000 = Rp Z
(Rp 750.000 x 40%) : 60 % = Rp 500,000

Jadi Harga awal adalah Rp 750,000 + Rp 500,000 = Rp 1,250,000

Jadi harga awal dari kulkas tersebut sebelum dipotong diskon adalah Rp 1,250,000

Demikianlah penjelasan singkat mengenai Cara Menghitung Harga Barang Setelah Diskon semoga kalian dapat memahaminya dengan baik. Mohon maaf apabila ada kesalahan di salam penulisan kata ataupun di dalam perhitungan angka-angka yang ada di dalam penjelasan di atas. Atas perhatian dan kesediaannya membaca artikel ini sampai akhir kami ucapkan terima kasih.

Cara Menyelesaikan Operasi Hitung Campuran Pada Bilangan Bulat

Operasi hitung campuran pada bilangan bulat seringkali muncul di dalam soal ulangan semester bahkan ujian nasional. Oleh karenanya, memahami konsep operasi hitung campuran menjadi penting untuk dipelajari. Seringkali siswa salah dalam mengerjakan soal-soal seperti ini karena tidak mengetahui bagian mana yang harus diselesaikan terlebih dahulu. Kita ambil contoh soal berikut ini:

Berapakah hasil dari (-5 + 7) x (-1 - 2) ....

A. 10

B. -10

C. -2

D. 50

Apakah kalian mengetahui jawaban dari soal tersebut? Terkadang masih saja ada yang kebingungan dalam mengerjakan soal-soal seperti ini karena tidak mengetahui apakah harus menyelesaikan per-kalian, pembagian, pengurangan, atau penjumlahan-nya terlebih dahulu. Hal terpenting yang harus kalian perhatikan di dalam menjawab bentuk soal seperti di atas adalah tanda kurung serta sifat-sifat operasi hitung bilangan bulat.

Jikalau di dalam soal tersebut terdapat tanda kurung, maka operasi hitung yang ada di dalam tanda kurung tersebut harus kita selesaikan terlebih dahulu. Akan tetapi, di dalam beberapa soal mungkin kalian juga akan menemui operasi hitung campuran yang tidak diberi tanda kurung. Llau bagaimanakah cara mengerjakannya? Simak penjelasan Rumus Matematika Dasar berikut ini:

Sifat-Sifat Operasi Hitung pada Bilangan Bulat

Operasi pengurangan (-) dan penjumlahan (+) di anggap sama kuat, sehingga operasi yang terletak di sebelah kiri, diselesaikan terlebih dahulu.

Contoh:

(4 + 3) - 2 = 5

(4 - 3) + 2 = 3

Begitu juga dengan operasi pembagian (:) dan perkalian (-) dianggap sama kuat. Yang ada di sebelah kiri, diselesaikan terlebih dahulu.

Contoh:

(4 x 3) : 2 = 6

(4 : 2) x 5 = 10

Operasi pembagian (:) dan perkalian (x) posisinya lebih kuat dibandingkan operasi pengurangan (-) dan penjumlahan (+) sehingga operasi perkalian dan pembagian diselesaikan terlebih dahulu, barulah operasi penjumlahan dan pengurangan.

Contoh:

20 + (2 x 3) = 26

20 - (10 x 2 : 5) + 5 => 20 - 4 + 5 = 21

Coba perhatikan Soal di bawah ini:

20 x 4 + 30 : 5 = 86

20 x (4 + 30) : 5 = 136

(20 x 4 + 30) : 5 = 22

20 x (4 + 30 : 5) = 136

Meski pun angka serta operasi hitung nya sama, ternyata hasilnya akan berbeda bergantung kepada adanya tanda kurung di dalam soal tersebut. Jadi sekali lagi kalian harus mengingat dengan baik bahwa di dalam menyelesaikan operasi hitung campuran pada bilangan bulat, kalian harus mengamati adanya tanda kurung atau tidak di dalam soal tersebut. Apabila ada tanda kurung, maka perhitungan yang ada di dalam kurung tersebut harus diselesaikan terlebih dahulu. Namun, apabila di dalam soal itu tidak terdapat tanda kurung, kalian harus mengikuti sifat-sifat operasi hitung bilangan bulat yang sudah kami jelaskan di atas. Semoga membantu.