Unsur-Unsur, Volume dan Luas Permukaan Bangun Ruang (Balok dan Kubus)

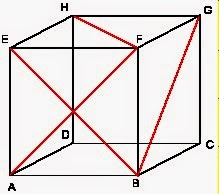
Balok

Balok adalah bangun ruang yang dibatasi oleh 6 persegi panjang atau persegi yang berimpit sisi-sisinya satu sama lain. Balok memiliki 3 pasang sisi yang sama dan sebangun dan paling sedikit mempunyai satu pasang yang tidak sama dan sebangun. Kedudukan pasangan sisi yang sama dan sebangun adalah sejajar. Balok mempunyai 6 sisi, 12 rusuk dan 8 titik sudut.

Benda-benda yang berbentuk seperti kemasan pasta gigi, lemari, kardus sepatu, akuarium, dan peti kemas.

Balok dapat digambarkan seperti berikut.

Unsur-Unsur Balok.

1.   Sisi-sisi balok berbentuk persegi panjang. Perhatikan sisi ABCD, EFGH, ABFE, CDHG, ADHE, dan BCGF. Sisi-sisi tersebut memiliki bentuk persegi panjang. Dalam balok, minimal memiliki dua pasang sisi yang berbentuk persegi panjang.


2.  Rusuk-rusuk yang sejajar memiliki ukuran sama panjang. Perhatikan rusuk-rusuk balok pada gambar diatas. Kelompok rusuk-rusuk yang sejajar sebagai berikut.
rusuk AB, CD, EF, dan GH, 
rusuk AE, BF, CG, dan DH, 
rusuk AD, BC, FG, dan EH.

3.   Setiap diagonal bidang pada sisi yang berhadapan memiliki ukuran sama panjang. Dari gambar terlihat bahwa panjang diagonal bidang pada sisi yang berhadapan, yaitu ABCD dengan EFGH (AC = BD = EG = FH), ABFE dengan DCGH (AF = BE = CH = DG), dan BCFG dengan ADHE (AH = ED = BG = CF).
  

4.   Setiap diagonal ruang pada balok memiliki ukuran sama panjang. Diagonal ruang pada balok ABCD.EFGH, yaitu AG, EC, DF, dan HB memiliki panjang yang sama. 

5.   Setiap bidang diagonal pada balok memiliki bentuk persegi panjang. Perhatikan balok ABCD.EFGH pada gambar dibawah ini. Bidang diagonal balok BDHF memiliki bentuk persegi panjang. Begitu pula dengan bidang diagonal lainnya. Pasangan-passangan bidang diagonal yang sama bentuk dan ukuran. 
Bidang ACGE = BDHF
Bidang ABGH = CDEF
Bidang ADFG = BCHE

Rumus Luas Permukaan dan Volume Balok

Luas Permukaan = L = 2 x (p x l + p x t + l x t)

Volume Balok        =  V = p x l x t


Contoh Soal:
1. Tentukan Luas permukaan dan Volume balok yang berukuran panjang 7 cm, lebar 5 cm dan tinggi 4 cm.
Jawaban:
 Luas Permukaan = L = 2 x (p x l + p x t + l x t)
                                       = 2 x (7 x 5 + 7 x 4 + 5 x 4)
                                       = 2 x (35 + 28 + 20)
                                       = 2 x 83
                                       =  168
Jadi luas permukaan balok adalah 168 cm².


Volume Balok    =  V = p x l x t
                                    = 7 x 5 x 4
                                     = 140
Jadi, volume balok adalah 140 cm³. 

2. Diketahui balok dengan volume 675 cm². Jika tinggi perbandingan panjang dan lebar 5 : 3 dan tinggi balok 5 cm, tentukan :
a. Ukuran panjang dan lebar
b. Luas permukaan balok.
Jawaban:
Misalkan panjang balok = 5n dan lebar balok = 3n 
Volume Balok    =  V = p x l x t
                           675  = 5n x 3n x 5
                            675 = 75 n².
                                  n = 3

a.  Panjang balok = 5 x 3 = 15 cm

     Lebar balok  = 3 x 3 = 9

b. Luas Permukaan = L = 2 x (p x l + p x t + l x t)                                        
                                       = 2 x (15 x 9 + 15 x 5 + 9 x 5)
                                       = 2 x (135 + 75 + 45)
                                       = 2 x 255
                                       = 510

Jadi, luas permukaan balok adalah 510 cm².





2.  Kubus

Kubus adalah bangun ruang yang dibatasi oleh 6 persegi  berukuran sama yang berimpit sisi-sisinya satu sama lain. Balok mempunyai 6 sisi, 12 rusuk dan 8 titik sudut.

Benda-benda yang berbentuk kubus seperti dadu dan rubrik mainan.

Kubus dapat digambarkan seperti berikut.

Unsur - unsur kubus.

a.         Kubus mempunyai 8 titik sudut, yaitu titik sudut A, B, C, D, E, F, G, dan H.

b.         Sisi-sisi kubus berbentuk persegi. Perhatikan sisi ABCD, EFGH, ABFE, CDHG, ADHE, dan BCGF. Pasangan sisi-sisi sejajar sebagai berikut: ABCD dan EFGH. ADHE dan BCGF, serta ABFE dan CDHG.

c.         Rusuk-rusuk yang berjumlah 12 berukuran sama. Perhatikan rusuk-rusuk kubus pada gambar di atas. Kelompok rusuk-rusuk yang sejajar.

1)     Rusuk AB, CD, EF, dan GH.

2)     Rusuk AE, BF, CG, dan DH.

3)     Rusuk AD, BC, FG, dan EH.

d.         Kubus mempunyai 12 diagonal bidang yang berukuran sama. Diagonal bidang kubus antara lain: AC, BD, AF,BE, BG, CF,CH, DG, AH, DE, EG, dan FH. Adapun pasangan diagonal bidang yang sejajar sebagai berikut.

           1)    AC  sejajar dengan EG

           2)    BD  sejajar dengan FH

           3)    AF  sejajar dengan DG

           4)    BE  sejajar dengan CH

           5)    AH  sejajar dengan BG

            6)    DE  sejajar dengan CF

e.         Kubus mempunyai 6 bidang diagonal yang berukuran sama. Bidang diagonal berbentuk persegi panjang. Bidang diagonal tersebut antara lain: ABGH, CDEF, ADGF, BCHE, ACGE, dan BDHF.

f.          Kubus mempunyai 4 diagonal ruang. Diagonal ruang adalah garis di dalam kubus yang menghubungkan  titik sudut dengan titik sudut di hadapannya yang tidak satu sisi. Setiap diagonal ruang pada kubus memiliki ukuran sama panjang. Diagonal ruang pada kubus ABCD.EFGH, yaitu AG, EC, DF, dan HB.

 

Luas Permukaan dan Volume Kubus

Luas = 6 x s x s = 6 s², dengan s = panjang rusuk kubus

Volume = s x s x s = s³

Contoh Soal
1. Tentukan volume dan luas permukaan kubus yang mempunyai panjang rusuk 8 cm.

Jawaban:
 Volume = s x s x s
               = 8 x 8 x 8
               = 512
Jadi, volume kubus adalah 512  cm³.

Luas Permukaan = 6 x s x s
                              = 6 x 8 x 8
                              = 384
Jadi, luas permukaan kubus adalah 384 cm².


2.  Diketahui kubus dengan volume 1.728  cm³. Tentukan luas permukaan kubus tersebut.

Jawaban:

 Volume = s x s x s
   1.728  = s³
          s  = 12 cm

Luas Permukaan = 6 x s x s
                              = 6 x 12 x 12
                              = 864
Jadi, luas permukaan kubus adalah 864 cm²

3. Sebuah kubus mempunyai panjang rusuk 6 cm. tentukan:
    a. panjang diagonal sisi
    b. panjang diagonal ruang
    c. Luas bidang diagonal
 
  Jawaban:
    a. Panjang diagonal sisi = sV2       (V  adalah tanda akar)
                                              = 6 V2 cm

    b. Panjang diagonal ruang = sV3
                                                  = 6V3 cm

   c. Luas Bidang diagonal = sisi x panjang diagonal sisi
                                              = 6  x  6V2
                                              = 36V2 cm2

Itulah beberapa penjelasan tentang Balok dan Kubus.
Selamat belajar.

 

Sistem Pertidaksamaan Linear Dua Variabel Kelas X SMA

Sistem Pertidaksamaan Linear Dua Variabel - Jika sebelumnya Rumus Matematika Dasar telah memberikan pembahasan materi mengenai sistem persamaan linear dua variabel, untuk melengkapi materi pelajaran matematika yang ada di SMA maka untuk postingan kali ini dihadirkan materi lanjutan mengenai sistem pertidaksamaan linear dua variabel. Pada materi di bawah ini akan dijabarkan mengenai pengertian, contoh soal, Serta pembahasan tentang sistem pertidaksamaan dua variabel. So, perhatikan dengan baik penjelasan materi matematika berikut ini:

Pertidaksamaan linear dapat diartikan sebagai sebuah pertidaksamaan dimana peubah bebasnya memiliki bentuk linear (berpangkat satu). coba kalian ingat lagi bentuk-bentuk pertidaksamaan berikut ini:

3x = 6 (pertidaksamaan linear dengan satu peubah)

2x + y < 0 (Pertidaksamaan linear dengan dua peubah)

2x + 3y - 4z >0 (Pertidaksamaan linear dengan tiga peubah)

Pda postingan ini saya akan membatasi penjelasan hanya pada pertidaksamaan linear dua peubah. Gabungan dari dua atau lebih pertidaksamaan linear dengan dua peubah dapat disebut sebagai pertidaksamaan linear dua variabel. Contoh dari sistem persamaan linear dua variabel adalah:

2x + 4y ≥ 16

x + y ≥ 8

x ≥ 0

y ≥ 0

Himpunan dan Daerah Penyelesaian Pertidaksamaan Linear Dua Variabel

Berikut ini adalah cara yang dapat dilakukan untuk menentukan himpunan ataupun daerah penyelesaian dari sistem pertidaksamaan dua variabel: ax + by ≤  c

Pertama, buatlah garis ax + by = c dengan cara menentukan dua titik yang berbeda pada garis tersebut di dalam diagram cartesius. Diagram kartesius nantinya akan terbagi menjadi dua bagian yang dipisahkan oleh garis itu.

Kedua, Lakukan subtitusi terhadap sebuah titik pada salah satu bagian ke dalam sistem pertidaksamaan tersebut. Jikalau hasilnya merupakan pernyataan yang benar, artinya daerah tersebut merupakan penyelesaiannya, akan tetapi bila pernyataanya salah maka bagian lain lah yang menjadi penyelesaiaanya.

Ketiga, arsirlah pada bagian yang menjadi daerah penyelesaian.

Untuk lebih jelasnya, perhatikan contoh soal berikut ini:

Contoh Soal 1

Coba tentukanlah daerah penyelesaian yang memenuhi sistem pertidaksamaan 2x + 3y ≤ 12

Jawab :

Gambar garis 2x + 3y ≤ 12, pilih dua titik

Apabila x = 0 maka :

2.0 + 3y = 12

3y = 12 

y = 4 titik (0,4)

Apabila y = 0 maka:

2x + 3.0 = 12

2x = 12 

x = 6 titik (6,0)

Pertama, pilihlah titik (0,0) kemudian subtitusikan titik tersebut ke dalam pertidaksamaan 2x + 3y ≤ 12. dari perhitungan di atas diketahui hasilnya adalah 2 x 0 + 3 x 0 ≤ 12 atau 0≤ 12 sehingga pernyataannya bisa dianggap benar. Sehingga dapat disimpulkan bahwa daerah penyelesaian dari pertidaksamaan tersebut berada pada daerah yang ada di bawah garis sampai kepada garis yang menjadi batas 2x + 3y = 12. Sehingga gambarnya menjadi:

Untuk kali ini cukup sekian dulu materi tentang Sistem Pertidaksamaan Linear Dua Variabel Kelas X SMA. Pada postingan selanjutnya mungkin akan dibahas lebih lanjut mengenai materi-materi yang berkaitan dengan system pertidaksamaan linear dua variable. Oleh sebab itu, ikuti terus materi pelajaran matematika yang diposting di dalam blog ini agar kalian tidak ketinggalan untuk bisa mempelajari beragam pembahasan materi matematika yang ada di blog ini.

Contoh Soal Try Out Matematika SMP Ujian Nasional Kelas 9

Contoh Soal Try Out Matematika SMP - Alhamdulillah, pada akhirnya Rumus Matematika Dasar dapat memberikan sebuah artikel yang berisi contoh soal ujian nasional untuk siswa SMP kelas 9. Semoga contoh soal try out yang diberikan di bawah ini mampu membantu kalian semua yang duduk di bangku SMP kelas 9 sebagai sarana latihan dalam rangka menghadapi ujian nasional. Soal ini berisikan beragam materi mulai dari faktorisasi aljabar, sampai materi mengenai himpunan. Harapannya adalah agar contoh soal ini bisa kalian gunakan untuk belajar dan mempersiapkan diri sebelum melaksanakan UN sehingga dapat memperoleh nilai yang memuaskan. Yuk mari langsung saja kita lihat contoh soal try out matematika berikut ini:

Contoh Soal Try Out Ujian Nasional Matematika SMP

Soal 1

Hasil  penjumlahan dari 5x + 3y - 4 dengan x - 5y - 1 adalah...

a. 6x - 2y - 5

b. 6x - 8y - 5

c. 6x - 2y + 4

d. 6x - 2y + 5

Soal 2

Bentuk faktor dari 6x² - 7x - 10 adalah ...

a. (x - 2)(6x + 5)

b. (x + 2)(6x - 5)

c. (2x - 5)(3x + 2)

d. (2x + 5)(3x - 2)

Soal 3

Hasil dari (5x - 7)(2x + 4) adalah ...

a. 10x²- 34x - 28

b. 10x²+ 34x - 28

c. 10x²- 6x - 28

d. 10x²+ 6x - 28

Soal 4

Hasil dari     3     +    5     adalah ...

                x + 5      x - 3

a.    8x + 16__

   (x + 5)(x - 3)

b.    5x + 16__

   (x + 5)(x - 3)

c.    3x – 16__

   (x + 5)(x - 3)

d.     8x + 8 ­­­­­­­­­­­__

   (x + 5)(x - 3)

Soal 5

Bentuk paling sederhana dari 2x² + 15 - 27 adalah ...

                                                  4x² - 9

a.   x – 9_

    2x - 3

b.   x + 9_

    2x + 3

c.   x + 3_

    2x + 1

d.   x + 3_

    2x + 3

Soal 6

Bentuk sederhana dari          3         -            2_      adalah …

                                      x2 + x - 2      x2 + 3x + 2

a.            x + 5_____

   (x + 2)(x + 1)(x -1)

b.            x + 1_____

   (x + 2)(x + 1)(x -1)

c.             x – 5_____

   (x + 2)(x + 1)(x -1)

d.              x – 1____

   (x + 2)(x + 1)(x -1)

Soal 7

Diagram panah untuk relasi faktor dari dari A = {2, 3, 5, 7} ke B = {6, 9, 10} adalah ...

Soal 8

(i).{(3,2),(4,3),(5,4),(6,5)}

(ii).{(6,1),(7,2),(8,1),(6,3)}

(iii).{(8,a),(6,b),(8,c),(4,d)}

(iv).{(p,q),(q,r),(p,s),(t,s)}

Himpunan pasangan berututan di atas yang merupakan fungsi adalah ...

a. (i)

b. (ii)

c. (iii)

d. (iv)

Semoga Contoh Soal Try Out Matematika SMP Ujian Nasional Kelas 9 yang sudah di-share di atas, bisa bermanfaat bagi adik-adik sekalian. Semoga sukses dan mampu menjawab soal-soal matematika di dalam ujian nasional dengan baik.

5 Contoh Soal Cerita Aljabar Matematika

Contoh Soal Cerita Aljabar Matematika - Materi pelajaran matematika mengenai aljabar bisa dibilang gampang-gampang susah. Jika kalian sudah memahami setiap konsep dan sifat aljabar tentu akan mudah dalam mengerjakan soal-soalnya. Akan tetapi untuk kalian yang belum memahami pengertian aljabar, tentu akan sulit dalam mengerjakannya. Ya, mempelajari meteri ini memang membutuhkan konsentrasi dan kecermatan dalam menghafalkan pola-pola perhitungan di dalam aljabar.

Nah, untuk melatih kemampuan kalian di dalam megerjakan soal-soal yang berkaitan dengan materi matematika mengenai aljabar, tidak ada salahnya apabila kalian mencoba untuk menyelesaikan soal-soal yang diberikan oleh Rumus Matematika Dasar di bawah ini. Soal ini agak berbeda kerena disajikan dalam bentuk soal cerita sehingga kalian harus memperhatikan dengan baik setiap simbol dan angka-angka yang terdapat di dalam soal tersebut agar nantinya kalian tidak melakukan kesalahan di dalam menjawab soal-soal tersebut.

Kumpulan Contoh Latihan  Soal Cerita  Matematika Mengenai Aljabar

Soal 1

Diketahui panjang dari sebuah persegi panjang adalah (2x - 5) cm sedangkan lebarnya adalah (3x + 1), Maka tentukanlah:

a. Keliling persegi panjang yang dinyatakan dalam x

b. ukuran persegi panjang apabila diketahui kelilingnya adalah 23 cm

Soal 2

Lima tahun yang lalu, usia seorang ibu beserta kedua anak kembarnya adalah 40 tahun. Apabila pada saat itu usia sang ibu adalah 30 tahun, Maka berapakah umur dari masing-masing anak kembarnya saat ini?

Soal 3

Pak Budi melakukan sebuah perjalanan keluar kota. awalnya ia mengendarai motor selama 3 jam dengan kecepatan rata-rata (2x - 5)km/jam. Setelah itu pak ketut melanjutkan perjalanan dengan menaiki bus selama 4 jam dengan kecepatan rata-rata (5x + 8) km/jam. Maka tentukanlah:

a. Jarak yang ditempuh dalam x

b. nilai x apabila jarak yang ditempuh adalah 329km

Soal 4

Sebuah model kerangka balok dibuat dari kawat dengan ukuran panjang (2x - 3) cm, lebar (3x + 10) cm dan tinggi x cm. tentukanlah:

a. Panjang kawat dalam x

b. nilai x jika panjang kawat adalah 388cm

c. ukuran kerangka balok

Soal 5

Di sebuah meja terdapat 5 sendok, 5 piring, dan 5 gelas. Budi mengambil 1 buah sendok dan piring. Lalu Ani menaruh 2 buah piring, 3 sendok, dan 1 gelas. Maka berapakah jumlah peralatan makan yang tersedia di meja tersebut sekarang?

Itulah 5 buah Contoh Soal Cerita Aljabar Matematikayang bisa kalian manfaatkan untuk melatih diri dalam memahami bagaimana cara menggunakan konsep-konsep aljabar di dalam menjawab soal. Semoga bisa membuat kalian semakin paham dan mahir dengan materi mengenai aljabar yang diberikan dan diajarkan oleh guru kalian di sekilah.